
What is PyAutoLens?#
When two or more galaxies are aligned perfectly down our line-of-sight, the background galaxy appears multiple times.
This is called strong gravitational lensing and PyAutoLens makes it simple to model strong gravitational lenses.
Getting Started#
The following links are useful for new starters:
The PyAutoLens readthedocs, which includes an installation guide and an overview of PyAutoLens’s core features.
The introduction Jupyter Notebook on Binder, where you can try PyAutoLens in a web browser (without installation).
The autolens_workspace GitHub repository, which includes example scripts and the HowToLens Jupyter notebook lectures.
Strong Gravitational Lensing#
When two galaxies are aligned down the line-of-sight to Earth, light rays from the background galaxy are deflected by the intervening mass of one or more foreground galaxies. Sometimes its light is fully deflected around the foreground galaxies, traversing multiple paths to the Earth, meaning that the background galaxy is observed multiple times. This alignment of galaxies is called a strong gravitational lens, an example of which, SLACS1430+4105, is shown in the image below. The massive elliptical lens galaxy can be seen in the centre of the left panel, surrounded by a multiply imaged source galaxy whose light has been distorted into an ‘Einstein ring’. The central and right panels shows reconstructions of the source’s lensed and unlensed light distributions, which are created using a model of the lens galaxy’s mass to trace backwards how the source’s light is gravitationally lensed.
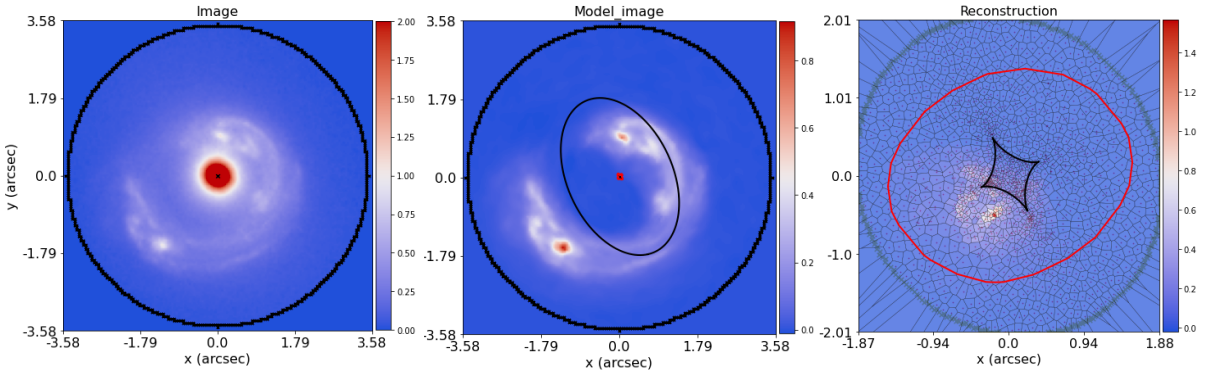
Strong lensing provides astronomers with an invaluable tool to study a diverse range of topics, including the structure of galaxies, dark matter and the expansion of the Universe.
The past decade has seen the discovery of many hundreds of new strong lenses, however the modeling of a strong lens is historically a time-intensive process that requires significant human intervention to perform, restricting the scope of any scientific analysis. In the next decade of order of one hundred thousand strong lenses will be discovered by surveys such as Euclid, the Vera Rubin Observatory and Square Kilometer Array.
The goal of PyAutoLens is to enable fully automated strong lens analysis, such that these large samples of strong lenses can be exploited to their fullest.
How does PyAutoLens Work?#
A strong lens system can be quickly assembled from abstracted objects. A Galaxy object contains one or
more LightProfile’s and MassProfile’s, which represent its two dimensional distribution of starlight and mass.
Galaxy’s lie at a particular distance (redshift) from the observer, and are grouped into planes. Ray tracing
through multiple planess is achieved by passing them to a Tracer with an astropy Cosmology. By passing
these objects a Grid2D strong lens sightlines are computed, including multi-plane ray-tracing. All of these
objects are extensible, making it straightforward to compose highly customized lensing system. The example code
below shows this in action:
import autolens as al
import autolens.plot as aplt
from astropy import cosmology as cosmo
"""
To describe the deflection of light by mass, two-dimensional grids of (y,x) Cartesian
coordinates are used.
"""
grid = al.Grid2D.uniform(
shape_native=(50, 50),
pixel_scales=0.05, # <- Conversion from pixel units to arc-seconds.
)
"""
The lens galaxy has an elliptical isothermal mass profile and is at redshift 0.5.
"""
mass = al.mp.Isothermal(
centre=(0.0, 0.0),
ell_comps=(0.1, 0.05),
einstein_radius=1.6
)
lens_galaxy = al.Galaxy(redshift=0.5, mass=mass)
"""
The source galaxy has an elliptical exponential light profile and is at redshift 1.0.
"""
disk = al.lp.Exponential(
centre=(0.3, 0.2),
ell_comps=(0.05, 0.25),
intensity=0.05,
effective_radius=0.5,
)
source_galaxy = al.Galaxy(redshift=1.0, disk=disk)
"""
We create the strong lens using a Tracer, which uses the galaxies, their redshifts
and an input cosmology to determine how light is deflected on its path to Earth.
"""
tracer = al.Tracer(
galaxies=[lens_galaxy, source_galaxy],
cosmology = al.cosmo.Planck15()
)
"""
We can use the Grid2D and Tracer to perform many lensing calculations, for example
plotting the image of the lensed source.
"""
tracer_plotter = aplt.TracerPlotter(tracer=tracer, grid=grid)
tracer_plotter.figures_2d(image=True)
To perform lens modeling, PyAutoLens adopts the probabilistic programming
language PyAutoFit. PyAutoFit allows users to compose a
lens model from LightProfile, MassProfile and Galaxy objects, customize the model parameterization and
fit it to data via a non-linear search (e.g. dynesty,
emcee or PySwarms). The example
code below shows how to setup and fit a lens model to a dataset:
import autofit as af
import autolens as al
import autolens.plot as aplt
"""
Load Imaging data of the strong lens from the dataset folder of the workspace.
"""
dataset = al.Imaging.from_fits(
data_path="/path/to/dataset/image.fits",
noise_map_path="/path/to/dataset/noise_map.fits",
psf_path="/path/to/dataset/psf.fits",
pixel_scales=0.1,
)
"""
Create a mask for the imaging data, which we setup as a 3.0" circle, and apply it.
"""
mask = al.Mask2D.circular(
shape_native=dataset.shape_native,
pixel_scales=dataset.pixel_scales,
radius=3.0
)
dataset = dataset.apply_mask(mask=mask)
"""
We model the lens galaxy using an elliptical isothermal mass profile and
the source galaxy using an elliptical sersic light profile.
To setup these profiles as model components whose parameters are free & fitted for
we set up each Galaxy as a `Model` and define the model as a `Collection` of all galaxies.
"""
# Lens:
mass = af.Model(al.mp.Isothermal)
lens = af.Model(al.Galaxy, redshift=0.5, mass=lens_mass_profile)
# Source:
disk = af.Model(al.lp.Sersic)
source = af.Model(al.Galaxy, redshift=1.0, disk=disk)
# Overall Lens Model:
model = af.Collection(galaxies=af.Collection(lens=lens, source=source))
"""
We define the non-linear search used to fit the model to the data (in this case, Dynesty).
"""
search = af.Nautilus(name="search[example]", n_live=50)
"""
We next set up the `Analysis`, which contains the `log likelihood function` that the
non-linear search calls to fit the lens model to the data.
"""
analysis = al.AnalysisImaging(dataset=dataset)
"""
To perform the model-fit we pass the model and analysis to the search's fit method. This will
output results (e.g., dynesty samples, model parameters, visualization) to hard-disk.
"""
result = search.fit(model=model, analysis=analysis)
"""
The results contain information on the fit, for example the maximum likelihood
model from the Dynesty parameter space search.
"""
print(result.samples.max_log_likelihood())
Getting Started#
To get started, users can check-out the PyAutoLens’s rich feature-set by going through the overview section
of our readthedocs. This illustrates the API for all of PyAutoLens’s core features, including how to simulate
strong lens datasets, reconstructing the lensed source galaxy on adaptive pixel-grids and fitting interferometer
datasets.
For new PyAutoLens users, we recommend they start by
installing PyAutoLens (if you haven’t
already!), read through the introduction.ipynb notebook on
the autolens_workspace and take the
HowToLens Jupyter notebook lecture series on
strong gravitational lensing.